Методы автоматизации составления расписания занятий. Часть 1: Классические методы оптимизации. А. Б. Сидорин, Л. В. Ликучева, А. М. Дворянкин
Одна из основных составляющих организации учебного процесса – это расписание занятий, которое регламентирует трудовой ритм подготовки студентов, влияет на творческую отдачу преподавателей, а также на эффективность использования ресурсов учебного заведения, таких как аудиторный фонд, вычислительная техника, оборудование лабораторий. С экономической точки зрения можно утверждать, что при оптимальном составлении расписания занятий уменьшатся постоянные затраты учебного заведения: электроэнергия, тепло, водоснабжение и т. п.
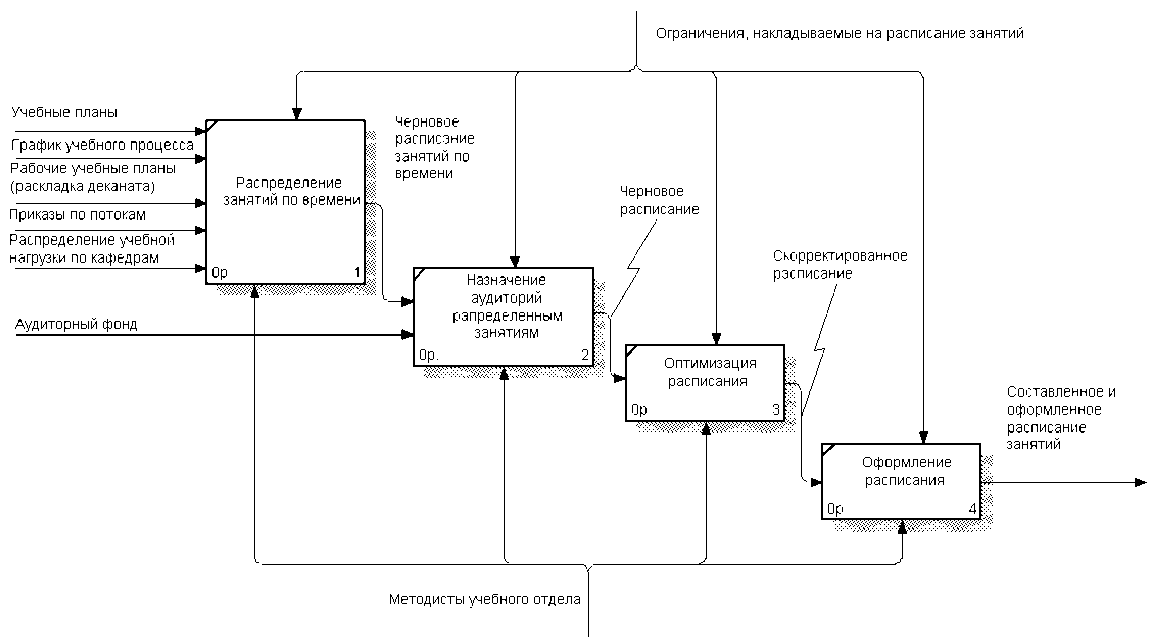
Процесс разработки расписания занятий можно представить следующей схемой бизнес процессов (см. рис.).
Вначале формируются все входные данные. Документы:
– «Учебные планы»;
– «График учебного процесса»;
– Рабочие учебные планы (раскладка деканата);
– «Приказы по потокам»;
– «Распределение учебной нагрузки по кафедрам»;
– Аудиторный фонд.
Далее методисты учебного отдела начинают составлять расписание:
1. Составление чернового варианта расписания
– Распределение занятий по времени;
– Назначение аудиторий распределенным занятиям.
2. Оптимизация расписания
– Корректировка расписания;
– Проверка расписания, исправление ошибок.
3. Оформление расписания
Выходом является готовое оформленное расписание.
Управляющим воздействием являются ограничения, накладываемые на расписание занятий.
Механизмом достижения цели являются методисты учебного отдела.
Для бизнес-процесса представленного на рис. 1 автоматизации могут подвергаться как отдельные этапы, так и все этапы вместе.
Проблеме автоматизации этих бизнес-процессов посвящена обширная литература [1, 3, 4, 7, 8, 9, 10, 14, 15, 16, 17, 18, 19, 22, 24, 29, 30] и созданы многочисленные инструментальные средства [9, 12, 13, 24].
Первые работы в области автоматизации составления расписания работ относятся к производственным системам и появились в 50–60-е гг. XX в. в связи с внедрением автоматизированных систем управления производством. Решение задач, связанных с составлением расписания выполнения работ в производственных системах привело к созданию теории решения задач составления расписаний (ЗСР) [1, 2, 3, 4]. Данная теория дает универсальные решения самых различных производственных задач, связанных с календарным планированием, упорядочением работ во времени и пространстве и др. с учетом имеющихся ограничений на располагаемые ресурсы. Решение задач составления расписания в рамках данной теории в конечном итоге сводится к использованию математического аппарата целочисленного программирования [7, 26, 27].
На рубеже XX и XXI веков актуальным стало создание систем автоматизированного управления учебным процессом в образовательных системах массового обучения (автоматизированных обучающих систем АОС). Связано это с усилением требований к качеству обучения, появлением разнообразных форм обучения, развитием форм дистанционного обучения, необходимостью повышения экономической эффективности обучения и др.
Первые работы в области автоматизации решения ЗСР для образовательных систем базировались на адаптации или модификации созданной в 50–60 гг. XX в. классической теории решения ЗСР применительно к решению задач составления расписания учебных занятий. Данный подход предусматривает формулировку задачи составления расписания занятий в терминах теории расписаний (выделение приборов и требований) с последующим решением ее одним из известных методов целочисленного программирования. В наиболее общей формулировке задача составления расписания в терминах теории расписания состоит в следующем. С помощью некоторого множества ресурсов или приборов должна быть выполнена некоторая фиксированная система требований (заданий). Цель заключается в том, чтобы при заданных свойствах требований и ресурсов и наложенных на них ограничениях найти эффективный алгоритм упорядочивания заданий, оптимизирующих или стремящийся оптимизировать требуемую меру эффективности. В известных работах, реализующих данный подход [5, 6, 11, 32, 35, 37], при формулировке задачи составления расписания учебных занятий в качестве приборов выступают аудитории, в качестве требований – учебные группы.
Необходимо отметить, что подобная формулировка и решение задачи составления расписания занятий с помощью аппарата классической теории расписаний связана с рядом сложностей и требует модификации (в том числе и терминологической) традиционной постановки ЗСР. Это выражается в необходимости учета специфических особенностей организации процесса обучения в образовательных системах. Так, в работах [24, 25] предлагается для решения задачи составления расписания учебных занятий использовать теоретический аппарат составления «производственных» расписаний. Это приводит к необходимости введения новых, зачастую искусственных понятий, таких как «многофункциональные приборы» и «комплексные требования», при этом в качестве приборов рассматриваются аудитории, а в качестве требований – занятия (в отличие от традиционного – учебные группы).
Необходимость такой модификации обусловлена спецификой образовательных систем: например, существуют такие виды занятий, которые проводятся одновременно для нескольких учебных групп (поточные лекции), а в рамках теории расписаний один прибор в некоторый момент времени не может обслуживать более одного требования.
Область эффективного применения известных методов составления «производственных» расписаний для составления расписания учебных занятий ограничена малыми образовательными системами с малым числом ограничений, накладываемым на расписание. Все это привело к появлению нового направления решения ЗСР учебных занятий, основанного на непосредственном использовании методов целочисленного программирования без привлечения методов традиционной теории составления «производственных» расписаний.
Все известные работы в этом направлении, посвященные автоматизации процедуры составления расписания занятий [1, 3, 4, 10, 22, 28, 29, 30, 31, 34, 35, 38, 39], можно условно разделить на две группы: к первой группе относятся работы, использующие классические методы: методы динамического программирования, целочисленного программирования, нелинейного программирования, методы имитационного моделирования: ветвей и границ [9], метод раскраски графа [7, 12], задача о назначениях [31] и др. Вторая группа работ основана на современных методах решения задач целочисленного программирования, использующих эвристические алгоритмы решения данных задач [7, 9, 13, 20, 21, 23, 33, 36].
Классические методы решения задачи составления расписания занятий
Отличительной чертой классических методов является достаточно высокая степень формализации (математическая строгость) как постановки задачи составления расписания занятий, так и алгоритмов ее решения (используются «жесткие» алгоритмы). Данные методы позволяют:
а) разрабатывать итеративные методы решения задачи составления расписаний учебных занятий, обладающие приемлемым временем сходимости и точностью решения;
б) оценивать влияние на время и точность решения задачи составления расписаний учебных занятий интересующих нас факторов.
Среди методов, используемых при составлении ЗСР занятий, можно также выделить методы, основанные на использовании математического аппарата теории графов. При использовании данных методов задача составления расписания занятий сводится к задаче раскраски графа.
В этом случае строится граф, в котором каждая вершина представляет собой запланированное учебным планом занятие. Если между какими-то двумя вершинами возможны конфликты (появляются накладки), например, два занятия проводятся в одной аудитории, то они соединяются ребром. Это эквивалентно запрету одновременного проведения этих занятий. Тогда задачу составления расписания можно сформулировать как задачу минимизации числа цветов, необходимых для раскраски графа, где каждый цвет соответствует одному периоду расписания [12].
Применение данного метода при решении реальных задач составления расписания для образовательных систем массового обучения малоэффективно, но сочетание данного подхода с другими методами может оказаться полезным [26, 27] .
Наиболее похожей постановкой задачи является задача о назначениях, которая является частным случаем транспортной задачи. Задача о назначениях имеет место при назначении людей на должности или работы, автомашин на маршруты, водителей на машины, при распределении групп по аудиториям, научных тем по научно-исследовательским лабораториям и т. п.
Задача о назначениях – это задача, в которой для выполнения каждой работы требуется один и только один ресурс (один человек, одна автомашина и т. д.), а каждый ресурс может быть использован на одной и только одной работе. То есть ресурсы не делимы между работами, а работы не делимы между ресурсами [31].
Специфическая структура задачи о назначениях позволила разработать так называемый «Венгерский метод» ее решения. Этот метод основан на симплекс-методе [10].
Общим недостатком всех классических методов является то, что они в своей основе используют итерационную процедуру поиска или улучшения некоторого начального приближения (опорного плана расписания), причем поиск результата осуществляется в окрестностях этого приближения. Это означает, что полученный результат напрямую зависит от некоторого начального приближения и естественно возникает проблема выбора ее значения.
Кроме того, организация поиска экстремума целевой функции в классических методах происходит:
во-первых, на основе изучения ее свойств в «малом» (в малой окрестности от начального приближения), можно сказать почти «в слепую»,
во-вторых – только в одном направлении, определяемом направлением желаемого изменения целевой функции в малой окрестности ее наблюдения.
Все это приводит к необходимости множественного эксперимента с разными значениями начального приближения, что существенно увеличивает время поиска окончательного решения.
Также недостатком классических методов является громоздкость и сложность получаемой математической модели и резкий (экспоненциальный) рост временных затрат на поиск приемлемого решения с ростом объемов исходной информации.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Конвей, Р. В. Теория расписаний [Текст] / Р. В. Конвей, В. Л. Максвелл, Л. В. Миллер– М.: Наука, 1975. – 395 с.
2. Танаев, В. С. Теория расписаний. Многостадийные системы [Текст] / В. С. Танаев, Ю. Н. Сотский, В. А. Струсевич – М.: Наука, 1989. – 256 с.
3. Танаев, В. С., Шкуба В. В. Введение в теорию расписаний [Текст] / В. С. Танаев, В. В. Шкуба – М.: Наука, 1975. – 256 с.
4. Строкина, Ю. Г. Алгоритмические процедуры формирования гетерогенных расписаний для производственных систем [Текст]: дис. на соискание ученой степени канд. техн. наук. – Уфа: УГАТУ, 1997, 150 с.
5. Бабкин, Э. А. Проектирование и реализация алгоритмов составления учебного расписания на основе многоагентных технологий. [Текст] / Э. А. Бабкин, И. М. Ретинский // Материалы научно-технической конференции. Технические, программные и математические аспекты управления сложными распределенными системами, Нижний Новгород, 2003, с. 10–12.
6. Безгинов, А. Н. Обзор существующих методов составления расписания [Текст] / А. Н. Безгинов, С. Ю. Трегубов // Информационные технологии и программирование: межвузовский сборник статей. Выпуск 2(14). – М.: МГИУ, 2005.
7. Маслов, М. Г. Эвристический алгоритм решения задачи составления расписания учебных занятий в вузе [Текст] М. Г. Маслов // Математические методы в технике и технологиях: Сб. трудов XV Международной научной конференции. В 10–и т. 2–4 июня 2002 г. – Тамбов, 2002. – Т. 9. – С. 86–88.
8. Вагнер, Г. Основы исследования операций. В 3 т. Т. 1. / Г. Вагнер; пер. с англ. Б. Т. Вавилова. – М.: Мир, 1972. – 335 с.
9. Вагнер, Г. Основы исследования операций [Текст]: в 3 т. Т. 2 / Г. Вагнер; пер. с англ. В. Я. Алтаева. – М.:Мир, 1973–488 с.
10. Вагнер, Г. Основы исследования операций [Текст]: в 3 т. Т. 3 / Г. Вагнер; пер. с англ. Б. Т. Вавилова. – М.: Мир, 1972–501 с.
11. Каширина, И. Л. Генетический алгоритм решения квадратичной задачи о назначениях специального вида [Текст] / И. Л. Каширина // Вестник ВГУ, 2003, № 1.
12. Клеванский, Н. Н. Формирование расписания с использованием динамических критериев загруженности [Текст] / Н. Н. Клеванский, Е. А. Макарцова // XI Международная конференция-выставка «Информационные технологии в образовании». Часть IV. – М.: МИФИ, 2001. – С.139–140.
13. Клеванский Н. Н. Моделирование стратегии формирования расписания занятий ВУЗ’а средствами реляционной алгебры [Текст] / Н. Н. Клеванский, Е. А. Макарцова, С. А. Костин // Прикладные проблемы образовательной деятельности: Межвуз. сб. научн. тр. Воронеж: ВГПУ, 2003. – С. 71–74.
14. Клеванский Н. Н. Анализ результатов автоматического формирования расписания занятий ВУЗ’а [Текст] / Н. Н. Клеванский, Е. А. Макарцова // XII Международная конференция-выставка «Информационные технологии в образовании». Часть IV. – М.: МИФИ, 2002. – С. 193.
15. Клеванский Н. Н. Использование графического представления в планировании расписания занятий [Текст] / Н. Н. Клеванский, Е. А. Макарцова, Д. И. Дудин // Совершенствование подготовки учащихся и студентов в области графики, конструирования и стандартизации: Межвуз. научн.-метод. сб. Саратов: СГТУ, 2002. – С. 113–114.
16. Клеванский Н. Н. Формирование оптимального расписания занятий ВУЗ’а и средства его визуализации [Текст] / Н. Н. Клеванский, С. А. Костин // Материалы XV Международной конференции «Применение новых технологий в образовании». – Троицк: «Байтик», 2004. – С. 380–382.
17. Гвоздев, Б. А. Составление расписаний в учебных заведениях: требования, проблемы, подходы к решению [Текст] / Б. А. Гвоздев, П. Г. Емельянов, Е. В. Пак // Институт систем информатики имени А. П. Ершова Сибирского отделения Российской академии наук, Новосибирский государственный университет.
18. The Influence of the Fitness Evaluation Method on the Performance of Multiobjective Optimisers [Text] / E. K. Burke, J. D. Landa Silva // To appear in European Journal of Operational Research – 2005.
19. Solving Examination Timetabling Problems Through Adaptation of Heuristic Orderings [Text] / E. K. Burke, J. Newall // Annals of operations Research – 2004 – Vol. 129, pp. 107–134.
20. Evolutionary Algorithms for Solving Multi-Objective Problems [Text] / C. A. Coello Coello, D. A. Van Veldhuizen, G. B. Lamont // Kluwer Academic Publishers – 2002.
21. An Investigation of a Hyper-heuristic Genetic Algorithm Applied to a Trainer Scheduling Problem [Text] / P. Cowling, G. Kendall, L. Han // Proceedings of the 2002 Congress on Evolutionary Computation (CEC 2002) – 2002 – pp. 1185–1190.
22. Hyperheuristics: A Robust Optimisation Method Applied to Nurse Scheduling [Text] / P. Cowling, G. Kendall, E. Soubeiga // Proceedings of the VII Parallel Problem Solving From Nature (PPSN VlI), Lecture Notes in Computer Science – 2002 – Vol. 2439, Springer, pp. 7–11.
23. Towards a Quick Computation of Well-Spread Pareto Optimal Solutions [Text] / K. Deb, M. Manikanth, S. Mishra // Proceedings of the 2nd International Conference on Evolutionary Multi-Criterion Optimization (EMO 2003), Faro Portugal, Lecture Notes in Computer Science – 2003 – Vol. 2632, Springer, pp. 222–236.
24. Fuzzy Optimality and Evolutionary Multiobjective Optimization [Text] / M. Farina, P. Amato // Proceedings of the 2nd International Conference on Evolutionary Multi-Criterion Optimization (EMO 2003), Faro Portugal, Lecture Notes in Computer Science – 2003 – Vol. 2632, Springer, pp. 58–72.
25. Distributed Choice Function Hyper-Heuristics for Timetabling and Scheduling [Text] / A. Gaw, P. Rattadilok, R. S. K. Kwan // Proceedings of the 2004 International Conference on the Practice and Theory of Automated Timetabling (PATAT 2004) – 2004. – Pittsburgh USA, pp. 495–497.
26. Multi-level Multi-objective Genetic Algorithm Using Entropy to Preserve Diversity [Text] / S. Gunawan, A. Farhang, Azarm 5 // Proceedings of the 2nd International Conference on Evolutionary Multi-Criterion Optimization (EMO 2003), Faro Portugal, Lecture Notes in Computer Science – 2003. – Vol. 2632, Springer, pp. 148–161.
27. Investigation of a Tabu Assisted Hyper-Heuristic Genetic Algorithm [Text]/ L. Han, G. Kendall //Proceedings of the 2003 Congress on Evolutionary Computation (CEC2003) – 2003 – Canberra Australia, pp. 2230–2237, IEEE Press.
28. Niche Distributions on the Pareto Optimal Front [Text] / J. Horn // Proceedings of the 2nd International Conference on Evolutionary Multi-Criterion Optimization (EMO 2003), Faro Portugal, Lecture Notes in Computer Science – 2003 – Vol. 2632, Springer, pp. 365–375.
29. Adaptive Diversity Maintenance and Convergence Guarantee in Multiobjective Evolutionary Algorithms [Text] / H. Jin, M.L. Wong // Proceedings of the 2003 Congress on Evolutionary Computation (CEC 2003) – 2003 – Camberra Australia, IEEE Press, pp. 2498–2505.
30. Improved Sampling of the Pareto-front in Multiobjective Genetic Optimization by Steady-state Evolution: A Pareto Converging Genetic Algorithm [Text] / R. Kumar, P. Rockett // Evolutionary Computation – 2002 – Vol. 10, No. 3, pp. 283–314.
31. Combining Convergence and Diversity in Evolutionary Multiobjective Optimization [Text] / M. Laumams, L. Thiele, K. Deb, E. Zitzler // Evolutionary Computation – 2002 – Vol. 10, No. 3, pp. 263–282.
32. The Role of e-dominance in Multi-objective Particle Swarm Optimization Methods [Text] / S. Mostaghim, J. Teich // Proceedings of the 2003 Congress on Evolutionary Computation (CEC 2003) – 2003 – Camberra Australia, IEEE Press, PP. 1764–1771.
33. Learning a Procedure that Can Solve Hard Binpacking Problems: A New GA-based Approach to Hyperheuristics [Text] / P. Ross, J. G. Marin-Blazquez, S. Schulenburg, E. Hart // Proceedings of the 2003 Genetic and Evolutionary Computation Conference (GECCO 2003), Lecture Notes in Computer Science – 2003. – Vol. 2724, Springer, pp. 1295–1306.
34. A Max-Min Ant System for the University Course Timetabling Problem [Text] / K. Socha, J. Knowles, M. Samples // Ant Algorithms: Proceedings of the Third International Workshop (ANTS 2002), Lecture Notes in Computer Science – 2002. – Vol. 2463, Springer, pp. 1–13.
35. Agent-based Evolutionary Mul-tiobjective Optimization [Text] / K. Socha, M. Kisiel-Dorohinicki // Proceedings of the 2002 Congress on Evolutionary Computation (CEC 2002) – 2002. – Hawaii USA, IEEE Press, PP. 109–114.
36. Development and Application of Hyperheuristics to Personnel Scheduling [Text] / E. Soubeiga // PhD Thesis, School of Computer Science and Information Technology, University of Nottingham, June 2003.
37. J. Thompson, K. Dowsland. «Variants of simulated annealing for the examination timetabling problem. Annals of Operational Research», 63, 1996.
38. University Timetabling [Text] / S. Petrovic, E. Burke // Handbook of Scheduling: Algorithms, Models, and Performance Analysis. – Chapman & Hall CRC – 2004. – P. 45.1– 45.23.
39. Recent Research Directions in Automated Timetabling [Text] / E. K. Burke, S. Petrovic // European Journal of Operational Research. 140(2):266–280, 2002.